1. 단측 검정이란?
단측 검정은 가설 검정에서 한 방향으로만 차이를 검증할 때 사용하는 방법.
- 오른쪽 단측 검정: 값이 기준보다 큰지 확인할 때
- 왼쪽 단측 검정: 값이 기준보다 작은지 확인할 때

단측검정 vs 양측검정 비교표
| 구분 | 양측 검정(Two-tailed Test) | 단측 검정 (One-tailed Test) |
| 유의수준 (α) | α = 0.05 → 양쪽으로 나눠 각 2.5%씩 분배 | α = 0.05 → 한쪽에 5% 집중 |
| 기준 Z값 | ±1.96 | 1.645 또는 -1.645 (검정 방향에 따라 선택) |
| 기각 기준 | Z값이 ±1.96을 벗어나면 귀무가설 기각 | Z값이 1.645 (또는 -1.645)를 넘으면 기각 |
| 신뢰구간 | 중앙 95% | 한쪽으로 95% |
| 사용 예시 | "평균이 다를까?" → 차이가 있는지 확인 | "평균이 더 클까/작을까?" → 특정 방향 확인 |
| 적합한 경우 | 차이가 "크거나 작다" 모두 중요할 때 사용 | 한쪽 방향의 차이만 중요할 때 사용 |
2. 기본 개념 정리
| 용어 | 설명 |
| 귀무가설 (H₀) | 기본 가정. "변화 없음" 또는 "주장대로이다" |
| 대립가설 (H₁) | 귀무가설이 틀렸다고 주장하는 가설. 검증하고 싶은 내용 |
| 유의수준 (α) | 제1종 오류 허용 한계. 보통 0.05 또는 0.01 사용 |
| 검정 통계량 (Z값) | 표본과 귀무가설의 차이를 수치화한 값 |
| 기각역 | Z값이 이 영역에 들어가면 귀무가설을 기각 |
| p-value | "이 정도 결과가 우연히 나올 확률" → 작을수록 귀무가설 기각 가능성 ↑ |
3. 예시 문제: 피자 토핑 검정 🍕
문제:
피자집 사장님은 “우리 피자에는 평균적으로 10개의 토핑이 올라간다”고 주장했다. 🍕
→ “진짜 그럴까? ” 🤔
→ 피자를 30판 주문, 토핑을 세어보니 평균 9 표준편차 1.5 였다.
사장님의 주장을 신뢰할 수 있는지 가설 검정을 해보자!
💡 주어진 데이터:
- 표본 평균(\bar X) = 9
- 모평균(μ) = 10 (사장님 주장)
- 표본 표준편차(s) = 1.5
- 표본 크기(n) = 30
- 유의수준(α) = 0.05 (단측 검정)
✔️ STEP 1: 가설 세우기
- 귀무가설(H₀): μ = 10 → 사장님의 말이 맞다
- 대립가설(H₁): μ < 10 → 사장님의 말이 틀렸다 (토핑이 적다)
✔️ STEP 2: Z-값 계산하기
Z-검정 공식:
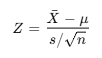
대입:

✔️ STEP 3: 기각 여부 판단
- 유의수준(α = 0.05) → 임계값(Critical Value) Z = -1.645
- 우리가 구한 Z = -3.65(🟢) : 임계값(🔴)보다 왼쪽에 있음 → 기각역에 해당!
4. 결과 해석 (그래프 참고):

- 🔴 빨간색 음영 → 기각역 (Z < -1.645)
- 🟢 초록색 점선 → 계산된 Z값 (Z = -3.65)
💡 결론:
- 기준선 Z = -1.645보다 왼쪽에 있는 결과(기각역에 위치) → 귀무가설 기각
- 계산된 Z = -3.65는 기각역 안(왼쪽)에 들어가기 때문에 → 귀무가설 기각! 🎉
- 사장님의 말은 통계적으로 틀렸다고 볼 수 있다! 🍕
5. p-value 해석
상황:
피자집 사장님은 "우리 피자엔 평균적으로 10개의 토핑이 올라간다!" 라고 말했다.
하지만 우리가 피자 30판을 사서 세어본 결과, 평균 9개의 토핑이 나왔다.
검정을 해봤더니, p-value ≈ 0.00013 이라는 결과가 나왔다.
- p-value ≈ 0.00013 → 매우 작음
- p < 0.05 → 귀무가설 기각 가능
Q1. p-value가 뭘 의미할까?
- 귀무 가설이 맞다고 가정했을 때, 관측된 결과가 나올 확률(어떤 사건이 우연히 발생할 확률)
🍕 피자 예시:
- 피자집 주장: 평균 토핑 10개
- 우리가 관측한 결과: 평균 토핑 9개
- p-value = 0.00013 → 주장이 맞다면 이런 결과가 나올 확률은 0.013%
🚫 틀린 해석:
- "사장님 말이 틀릴 확률이 99.987%다" ❌
- "앞으로 피자를 시키면 토핑이 적게 나올 확률이 99%다" ❌
🙆♀️올바른 해석:
- "사장님 말이 맞다고 가정했을 때, 이렇게 토핑이 적게 나올 확률은 0.013%밖에 안 돼!"
- "이런 일이 실제로 벌어졌으니, 사장님 말을 믿이 어렵다고볼 수 있다."
Q2. 유의수준(α)을 0.05로 잡았다면, 사장님 말은 어떻게 될까?
- 유의수준: 귀무 가설이 맞는데 잘못 기각할 확률
- α = 0.05 → "5% 이내로 드문 일이라면, 귀무가설을 기각할 수 있다!"
- p-value = 0.00013 → 0.05보다 훨씬 작음 → 귀무가설 기각!
→ "우리가 허용한 최대 오차인 5%보다 p-value가 훨신 작으니까, 이 결과는 '우연'으로 보기 어려워. 이건 진짜 우연이라기 보단, 사장님 말이 틀렸다고 보는게 맞아🙅♂️. 귀무가설을 기각할 수 있어!"
Q3. 왜 p-value가 작을수록 귀무가설을 기각할 수 있을까?
- p-value가 작을 수록 우연히 이런 결과가 나올 확률이 작기 때문: 주장이 틀리다고 보는 게 더 합리적
💡 해석:
"사장님 주장이 맞다면(μ = 10), 이 정도로 토핑이 적게 나올 확률은 0.013%밖에 안 되니까, (매우 드물게 일어나야 하는 일이 실제로 일어났으니) 사장님의 주장이 틀렸다고 보는 게 더 합리적이야! "
6. 요약
용어설명
| 귀무가설 (H₀) | μ = 10 : "피자 토핑 평균은 10개다" |
| 대립가설 (H₁) | μ < 10 : "피자 토핑 평균은 10개 미만이다" |
| 유의수준 (α) | "5% 확률 이내면 귀무가설 기각" |
| Z값 | -3.65 → 기각역 안쪽에 위치 |
| p-value | 0.00013 → 매우 유의미한 결과 |
| 결론 | 귀무가설 기각 → 사장님 말 틀렸다! 🍕 |
'통계' 카테고리의 다른 글
| 통계와 나 (0) | 2025.04.24 |
|---|---|
| [통계] 제 1종 오류(α) vs 제 2종 오류(β) (0) | 2025.02.27 |
| 통계적 가설 검정(Statistical Inferences) (1) | 2025.02.25 |
| [통계] 자유도(degree of freedom, d.f.) (2) | 2025.02.17 |