통계학을 공부하다 보면 종종 표본 분산(sample variance) 공식에서 "n-1"로 나누는 것을 보게 된다.
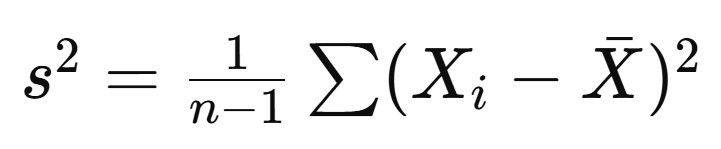
이때, 왜 n이 아니라 n-1로 나누는 걸까?
이건 '자유도' 때문이라고 설명한다.
그런데, 대체 이 자유도가 무엇이며 왜 하필 숫자 1을 빼주는 걸까?
자유도에 대해 알아보자.
1. 자유도의 정의
자유도(degree of freedom, d.f.)란 독립적으로 값을 선택할 수 있는 개수를 의미한다.
즉, 주어진 데이터에서 제약 없이 자유롭게 변할 수 있는 값의 수이다.
수식적으로는 다음과 같이 표현된다.
자유도 = 총관측치수(n) - 제약조건의 갯수
자유도가 중요한 이유는 통계적 검정에서 신뢰도를 결정하는 요소이기 때문이다.
특히 표본 분산과 t-분포에서 핵심적으로 작용한다.
2.자유도의 직관적인 이해
자동차 좌석 예시
(자유도라는 개념을 이해하기 위한 예시다.)
5명의 친구가 차를 타야 한다고 하자.
처음 4명은 원하는 좌석을 자유롭게 선택할 수 있지만, 마지막 1명은 남은 좌석에 앉아야만 한다.
즉, 자유롭게 선택할 수 있는 건 4명뿐 → 이런 상황에서 자유도는 4라고 볼 수 있다.
통계에서도 마찬가지다.
표본 평균이 주어지면 마지막 값은 자동으로 결정되므로 자유도가 줄어든다.
숫자로 보는 자유도 예시
세 개의 숫자(X1, X2, X3)가 있다고 하자.
- 제한 없이 아무 숫자나 고를 수 있다면 자유도는 3.
- 하지만 "이들의 평균이 10이다"라는 조건이 들어오면?
- X1, X2에는 아무런 값이나 와도 상관 없다.
- 하지만, 평균 10을 맞추기 위해서 X1, X2가 결정 된 후에
- X3 = 30 - (X1 + X2)로 결정된다.
- 즉, 자유롭게 선택할 수 있는 것은 두 개뿐 → 자유도는 2! 가 된다.
즉, 평균이 주어지면 평균이라는 제약조건이 생겨 자유도가 1 감소하게 된다!
3. 자유도는 왜 중요할까?
자유도가 중요한 이유
- 자유도는 통계 분석에서 신뢰도를 결정하는 중요한 요소!
- 특히 표본 분산과 t-분포에서 핵심적으로 작용한다.
표본 분산과 자유도 관계
표본 분산을 계산할 때, 우리는 모평균(μ)을 모른다. 대신 표본 평균(Xbar)을 사용해야 한다. 하지만 표본 평균 자체도 표본에서 계산된 값이므로, 독립적으로 결정할 수 있는 값이 하나 줄어든다.
즉, 표본에서 모분산을 추정할 때, 표본 평균을 이용해야 하기 때문에 하나의 값이 이미 결정된 상태가 된다. 따라서, 자유롭게 변할 수 있는 값이 하나 줄어들어 n 대신 n-1로 나누어 보정한다.
또한, 표본 크기가 작을수록 표본 평균과 모평균 사이의 차이가 커질 가능성이 높아진다. 따라서, 작은 표본에서는 변동성이 커지고 극단적인 값이 나올 확률도 높아진다. 이를 보정하기 위해 t-분포를 사용한다. 즉, t-분포는 표본 크기가 작을 때 표본 평균이 모평균과 다소 차이가 나는 불확실성을 반영하여, 신뢰구간을 더 넓게 잡아준다. 이렇게 함으로써 작은 표본에서도 보다 정확한 추론이 가능해진다.
4. 표준 정규분포 vs t-분포 (그래프 비교)
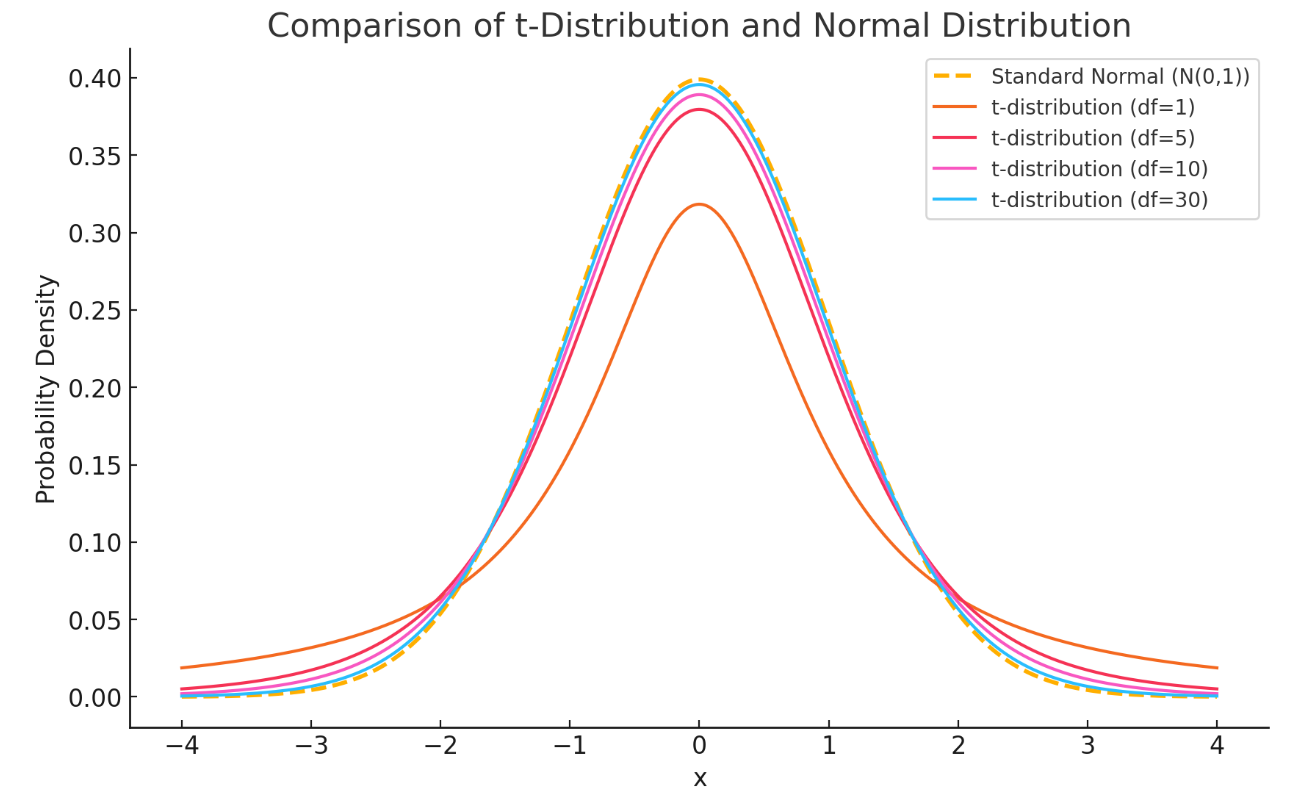
t-분포(t-Distribution)와 정규분포(Standard Normal Distribution)의 차이
- 자유도가 낮을수록 t-분포의 꼬리가 두껍다
→ 작은 표본에서는 변동성이 크기 때문에 정규분포 대신 t-분포를 사용한다. - 자유도가 커질수록 표본 평균과 모평균이 유사해지며, 분포의 형태가 점점 정규분포에 가까워진다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t, norm
# Define degrees of freedom
df_values = [1, 5, 10, 30]
x = np.linspace(-4, 4, 1000) # x-axis range
# Plot standard normal distribution
plt.plot(x, norm.pdf(x), label="Standard Normal (N(0,1))", linestyle="dashed", linewidth=2)
# Plot t-distributions for different degrees of freedom
for df in df_values:
plt.plot(x, t.pdf(x, df), label=f"t-distribution (df={df})")
# Configure the plot
plt.title("Comparison of t-Distribution and Normal Distribution")
plt.xlabel("x")
plt.ylabel("Probability Density")
plt.legend()
plt.grid()
# Show the plot
plt.show()
5. 정리
✔ 자유도란 "독립적으로 값을 선택할 수 있는 개수"
✔ 제약 조건이 생길수록 자유도는 감소
✔ 표본 평균을 사용하면 자유도 1 감소 → 그래서 표본 분산 계산 시 n-1로 나눈다
✔ 자유도가 낮을수록 t-분포의 꼬리가 두껍고, 자유도가 높으면 정규분포와 비슷해진다
✔ 표본 크기가 작을수록 변동성이 커지므로, 정규분포 대신 t-분포를 사용한다
'통계' 카테고리의 다른 글
| 통계와 나 (0) | 2025.04.24 |
|---|---|
| [통계] 제 1종 오류(α) vs 제 2종 오류(β) (0) | 2025.02.27 |
| [통계] 단측 검정(One-tailed Test) 이론 & 예시 (0) | 2025.02.26 |
| 통계적 가설 검정(Statistical Inferences) (1) | 2025.02.25 |